凯时KB88新闻网4月23日电(通讯员 邹志诚)近日���,航空科学与工程学院杨超教授团队在《航空学报》创刊60周年纪念专刊发表题为《RBF动网格技术研究进展及其气动弹性应用》的论文。绍了基于RBF的动网格技术基本理论���,分析了RBF方法的基函数与紧支半径选取方案���,对基于RBF的动网格技术的加速算法���、精度提升方法的研究进展进行了整理���,梳理了基于RBF的混合动网格技术。最后对目前气动弹性计算中基于RBF的动网格技术研究现状与发展前景做了简要总结。杨超教授为论文第一作者���,谢长川副教授担任论文通讯作者���,凯时KB88航空科学与工程学院为论文第一完成单位。

气动弹性问题起源于气动力���、弹性力���,惯性力三者间的相互作用。结构受气动载荷产生变形���,而结构变形又会改变气动载荷的大小与分布���,是一类典型的流固耦合问题。随着现代飞行器对航时���、速度等各类性能要求的日渐提升与各类新技术���、新理论的创新与发展���,气动弹性设计从过去的被动校核逐渐转变为主动设计���,成为飞机总体设计过程中不可或缺的重要部分���,并发挥着不可替代的关键作用。
气动力求解是气动弹性计算过程中的核心问题之一。得益于计算流体力学(Computational Fluid Dynamics���,CFD)技术的发展和计算机性能的大幅提高���,近年来的气动弹性计算正越来越多地采用以跨声速小扰动方程���、欧拉方程或Navier-Stokes方程为基础的CFD技术来计算气动力。CFD方法从流动基本方程出发���,使用的假设较少���,可以有效模拟流动的本质特征���,获得的气动力计算精度较高。在气动弹性计算过程中���,结构变形改变了流场的拓扑结构���,需要运用动网格技术来实现求解域的变形。因此���,动网格技术是气动弹性计算研究的关键技术���,发展通用性好���、计算效率高���、适用性强的动网格技术一直是气动弹性力学研究中广受关注的重点领域。
目前���,常用的动网格方法包括依托物理模型的弹簧类比法(Spring Analogy Method���,SAM)���、弹性体法(Elastic Solid Method���,ESM)和温度体法(Temperature Analogy Method���,TAM)等���,基于数学插值方法的超限插值法(Transfinite Interpolate���,TFI)���、逆距加权法(Inverse Distance Weighting���,IDW)���、Delaunay背景网格插值法(Delaunay Graph Mapping���,DGM)和径向基函数插值法(Radial Basis Function���,RBF)等���,以及各类混合方法。其中���,RBF方法的基本思想是由边界节点位移插值计算网格节点位移���,对结构网格和非结构网格均适用���,目前已在静气弹求解���、颤振计算等各类气动弹性问题的动网格计算中得到了较为广泛的应用���,展现了较强的变形能力���,被认为是一种具有较好应用前景的动网格计算方法。
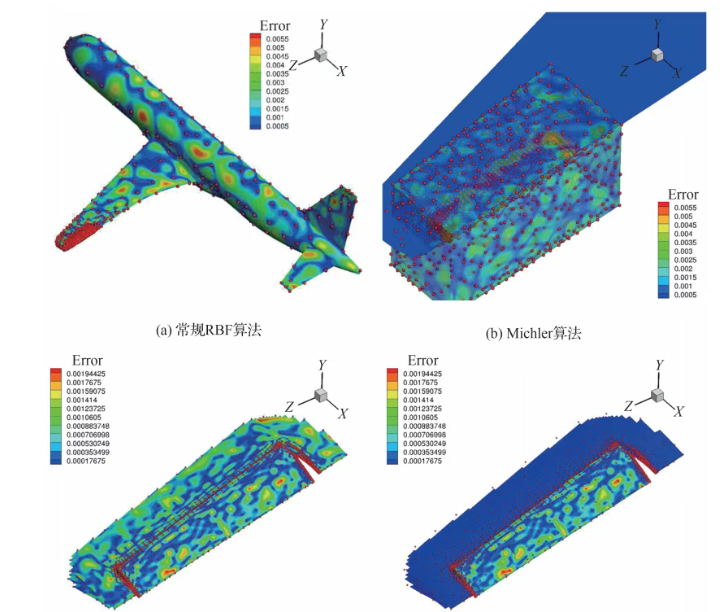
不同方法的插值点与计算误差对比
对于静气动弹性问题���,如果计算对象的构型较为简单���,如二维翼型���、长直机翼等���,则可以选择基础的RBF方法直接进行动网格计算。基础RBF方法实现最为简单���,且选取了所有物面插值点进行计算���,计算精度高���,可以对网格变形实现准确的计算���,为静气弹计算提供准确的计算结果。对于复杂构型���,贪心算法由于其原理简单���,实现难度低���,在复杂构型的静气弹动网格计算中应用最为广泛。对于几何非线性静气弹计算等大变形的情况���,可以采取动态控制点法等方法扩展RBF方法的变形能力���,满足大变形的计算需要。此外���,对于配平等各类仅需要仅对舵面等部分部件进行网格变形的问题���,可以采用区域限制法等方法对计算。
对于动气弹问题���,气动计算量大���,直接采用基础RBF方法开展动网格计算会带来计算量的显著增加���,严重影响计算效率。除二维问题外���,此类网格变形计算通常会采用贪心算法���、多级子空间法等方法精简插值点数量���,并在计算时采用并行计算以提升计算效率。其中���,贪心算法与并行计算由于操作简单���、技术成熟���,成为目前加速策略的主流选择。此外���,可以根据计算对象不同的气动网格类型���,选择RBF-TFI等效率更高的复合变形方法进行动网格计算���,尤其对于不太复杂的多块结构网格���,RBF-TFI方法可以在保证计算精度的情况下显著提高计算效率。
目前���,基于RBF方法的动网格计算理论与工程应用已较为成熟���,在各类气动弹性问题上都得到了广泛的应用。但是���,现有各类改进方法大部分存在实际应用难度较高���,改进后效率与鲁棒性难以兼得的缺陷。气动弹性问题大都涉及大量迭代计算���,而各类几何非线性气动弹性问题也对动网格的鲁棒性与计算精度提出了较高的要求。如何在RBF动网格计算中通过工程上易于实施的方法���,较好地兼顾计算效率与方法鲁棒性���,实现对大变形情况的高效高精度计算���,仍是有待研究解决的问题。为进一步适应气动弹性工程计算的需要���,RBF动网格计算的研究方向需要着重关注以下几点���:
1)对涉及多体运动���、前缘缝翼等较大相对运动与复杂相对运动的情况���,实现在网格变形计算过程中对变形网格实现自动化重构与加密���,保证适当的网格密度与网格质量���,避免因网格过于稀疏导致计算精度下降。
2)实现工程上易于操作的高效高精度RBF动网格计算方法���,减少使用方法过程中的人工操作���,在保证较高的计算精度与大变形适应能力的同时���,提升变形计算效率。
3)基于RBF方法开发模块化的网格变形工具���,以实现与不同气动力求解方法的耦合���,进而满足集成化设计的发展需要。
4)推导在工程上较为实用的降低控制方程矩阵Φ求解计算量的数学方法���,在不影响计算精度的同时���,从根源上降低RBF方法在大型网格计算中计算量显著增加的问题。
文章链接���:http://mp.weixin.qq.com/s/EF1_8v45LO0coDnYpd_Nqw
(审核���:董雷霆)
编辑���:贾爱平